The US CDC data reveals an interesting age-specific case versus deaths paradox. Look at the following graph. I created the graph using data available at the US CDC website. Of all the COVID-19 cases, 85.6 percent occurred among those aged equal and below 64 years. In contrast, of all the COVID-19 deaths, 80.6 percent occurred among those aged 65 and above. Now, my message is clear and straightforward based on this graph: Minimize the contact between these two age groups. How can we minimize the contacts between these two age groups? My suggestions are; Provide financial and other incentives to…

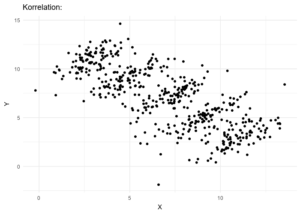
Simpson’s paradox may jeopardize your data interpretation.